大学生のおすすめバイト豆知識言いまーす。
バイトで一番おすすめなのは、大学で行われている実験の被験者バイト(これは良いですよ。これについてはまた記事を書きます。)
どうもこんにちは、某国立大化学科学部生のサブです。出だしは豆知識でスタートしました。くしゃみが止まらない状態でこの記事を書いています。
さてさて今回は、この記事の後編を書いていきたいと思います。前回は、化学科に入るにはぜひとも取り組んでおきたい大学数学の分野についてご紹介しました。今回はその続きをお送りしようと思います。(前回お示しした表を下に貼っておきますね。今回は、残りの緑と青の部分について説明していきます)

フーリエ変換
化学科に入ると、おそらく何度も耳にするであろう、このフーリエ変換。化学科に入って勉強やら実験やらを始めると、下のようなグラフに出会すことが幾度となくあるでしょう(私が実験で実際に自分でとった、ある化合物のIRスペクトルのデータです)。
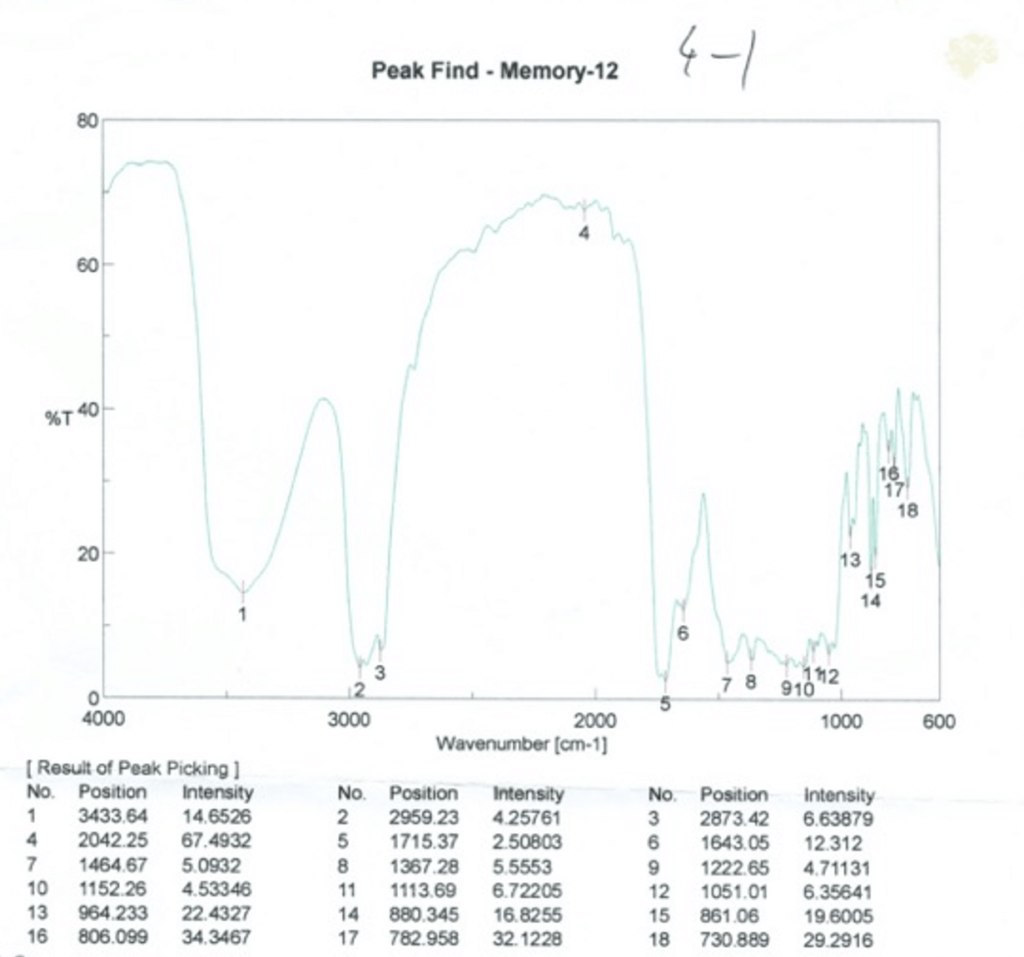
このグラフの横軸をよく見ると、Wavenumber(光の波長の逆数のことです。光の振動数と同じようなものです。)と書いてあります。このグラフは、化合物にある波数の光を当て、それをどの程度吸収したかを測定し、その波数を600から4000まで変化させた場合の吸収度合いを示しているのですが、実はこれにフーリエ変換が深く関わっているのです(原理としては、化合物に赤外線を当てて、当てた後の赤外線をフーリエ変換によって波数成分ごとの和で表現し、一つ一つの波数成分の強さがどれほど減少したか(=化合物によって吸収されたか)をグラフにした、という感じです)。化学科に入ると、このようなグラフを散々目にします。つまり、フーリエ変換と実質的に日夜を共にする状態になるわけです(これは言い過ぎですね笑)。しかし、これだけ関わるのですから、フーリエ変換について勉強するぐらいはしても良い気がします。しかしながら、このグラフ、もちろん機械が勝手に作ってくれるので、フーリエ変換についての知識がなくても、書くことはできてしまいます。そのせいか、化学科の学生の中でもフーリエ変換について理解しようとする人はほぼいない印象があります。
個人的な意見ですが、このような、数学的な原理を学ぼうとすることは絶対必要だと思っています。まして、周囲の人がやってないなら尚更です。そして、学んだことはすぐには役に立たないでしょう。しかし、修士や博士で必ずや役に立つはずです(自分がこのように思ったわけについてはまた記事を書くつもりです)。
話がずれてしまいました(笑)が、とにかく、フーリエ変換はぜひ取り組みましょう!(注. 数学科の方々がお買い上げされるような、ガチガチのフーリエ本を買う必要はありません。物理数学、という名前がついてるものを買うと良いでしょう)
群
これは量子化学の授業で必須の分野です。これがほどほどにわかっていないと詰みます。
化学科では、量子化学、という授業があり、そこでは電子くらいのミクロな系を数式で表現していく、ということをやるのですが、その授業で必ずと言って良いほど、指標表というものが扱われることになると思います。下のようなものです。
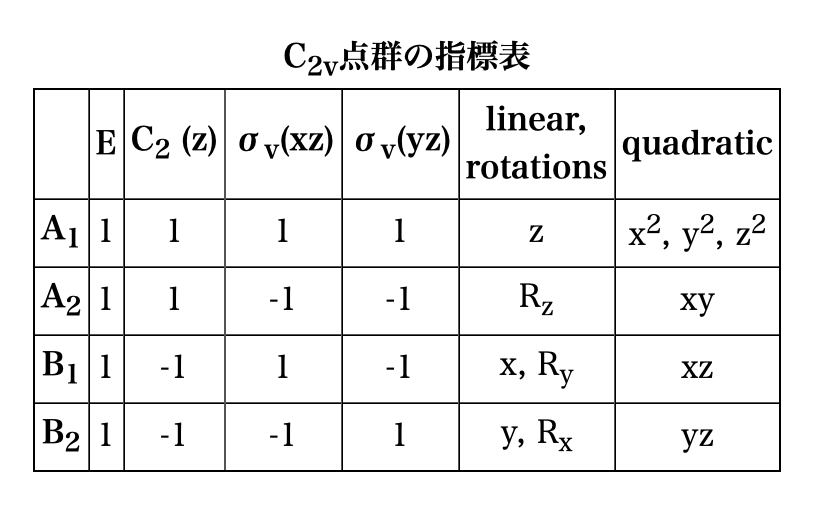
一見よくわからない表、と言った感じです。化学科の中でも、表面的でなく理解できている人はそうは多くありません。この表の理解には、初等的な群の知識が必須です。また、この表を用いると、様々なご利益があります。逆にいうと、この表がわからないと、後々、量子化学の授業や研究で、『うーん、なんかわからないなあ』というような事柄が増え、ずっともやもやした気持ちを抱えることになってしまいます。そうならないためにも、群についての知識はぜひとも身につけておきたいです。
ベクトル解析
書いていて思ったのですが、これは「余力があれば」のところに入れてもよかったですね、、笑
ベクトル解析は、電磁気学では必須なのですが、化学では必要になるシーンはほぼないです笑。ベクトル解析では、ベクトルに関する様々なことを学ぶのですが、その中で、ストークスの定理やガウスの発散定理というものが出てきます。これは今後大学でふと耳にすることがあるかもしれません。それらを理解するには、このベクトル解析を学ぶ必要があります。
ヤコビアン(追加)
すみません、これを忘れていました。これは、「余力があれば」に含まれるべきです。
ヤコビアンは、量子化学での、全空間での重積分の時に役立ちます。例えば、下のようなものです。
dxdydz=r^2sin\theta dr d\theta d\phi
この式、別にヤコビアンを理解していなくても、x,y,zをr,θ,φに変換したときの微小体積を考えれば導出できるのですが、背後には、ヤコビアンと呼ばれるものがあります。ヤコビアンを学べば、この場合に限らず、多様体論などで応用が効く(らしいです、、)ので、余力があればやってみるのも良いと思います。
ルジャンドル変換
これは、化学熱力学の裏側を覗きたくなったときにやってみるのが良いと思います。
熱力学では、平衡状態にある系の状態は、(U、V、N)(各々、系のエネルギー、体積、系に含まれる粒子数)で指定できるというのがもともとは経験的に定まっているのですが、場合によってはこの変数を他のものに変えることができます。その際に新たに定義される関数というのがありまして、それと他の熱力学関数とが、実はルジャンドル変換というもので結び付けられているのです(このことについては後々記事に書こうと思います)。
化学熱力学の授業では、P、V、Tが出てきた後に単に熱力学関数がポンポンと導入されていって、終わり!、みたいな感じになっていると思いますが、その”裏側”を知る上では、このルジャンドル変換は必須です。
複素関数論
これはオプションみたいなものですね。しかし、量子化学を勉強するなら学んでみても良いですね。
量子化学を学んでいくと、球面調和関数だとか、エルミート多項式とか、ラゲールの陪多項式だとか、そういう言葉に出会すでしょう。そして、それらについて調べてみると、「積分経路」、「正則」、「多価関数」とかいった言葉を目にするはずです(え、実数なのに積分経路もへったくりもあるの?と思われるかもしれません)。それらは、この複素関数論について学ぶことで意味がわかります。取り組んでみても良いですね。
以上で、全てのものを紹介してきました(学部生が主観で選んだものなので、あしからず)。私が化学科で体験してきたことなどを踏まえているので、未熟なりにも、同年代の方のお役に立てるのではないでしょうか。今後、このシリーズでは、前回と今回とで挙げた数学分野について概説していこうと思っています。
それでは、またまた〜。




