どうも、サブです。
今回は、つまずく人の多いであろう、時間に依存しない、初期状態に縮退があるときの摂動論の解説をしたいと思います。縮退のある摂動は、ハバード模型あたりになると直面することになるので、やっておいて損はないです。
縮退無しの場合の知識を前提とし、なるべく分かりやすく説明したいと思います。
まずは、簡単に問題設定を確認したいと思います。固有状態|n>及びその固有値EnがわかっているようなハミルトニアンH0に対し、摂動ハミルトニアンH’が加わることで|n>及びEnに生じる変化を、初期(無摂動)状態からのズレとして求めましょう、ということです。つまり、摂動ハミルトニアンが加わることで実数λを用いて
(H_0+{\lambda}H')\ket{{\psi}_n}=E_n'\ket{{\psi}_n}のように固有状態及び固有値が変化した時、固有状態と固有値を仮に
\ket{{\psi}_n}=\ket{n}+{\lambda}{\ket{n^{(1)}}}+{\lambda^2}{\ket{n^{(2)}}}+...\\\\E'_n=E_n+{\lambda}E_n^{(1)}+{\lambda}^2E_n^{(2)}+...のように初期状態を用いて表すと、どのようにズレは求められますか、ということです。
もし、Enが全てのnに対して異なっている(初期状態で縮退が完全にない)ならば、
E_n^{(1)}=\bra{n}H'\ket{n},\space\ket{n^{(1)}}=\sum_{k{{=}\mathllap{/\,}}n}\frac{\bra{k}H'\ket{n}}{E_n-E_k}\ket{k}\\E_n^{(2)}=\sum_{k\not = n}\frac{\bra{k}H'\ket{n}\bra{n}H'\ket{k}}{E_n-E_k}, \space\ket{n^{(2)}}=\sum_{k\not =n}[\sum_{l\not =n}\frac{\bra{k}H'\ket{l}\bra{l}H'\ket{n}}{(E_n-E_k)(E_n-E_l)}-\frac{\bra{k}H'\ket{n}\bra{n}H'\ket{n}}{(E_n-E_k)^2}]\ket{k}と書けるのでした。(下で定義される、|n>を除いた基底ベクトルで張られるベクトル空間への射影演算子Qnを使うとこの結果はもう少しスッキリと書けますが、詳細は割愛します)
Q_n=\sum_{k\not =n}\frac{\ket{k}\bra{k}}{E_n-H_0}次に、縮退が初期状態にて生じている場合を考えましょう。例えば、下のポンチ絵の右のような状況を考えます。
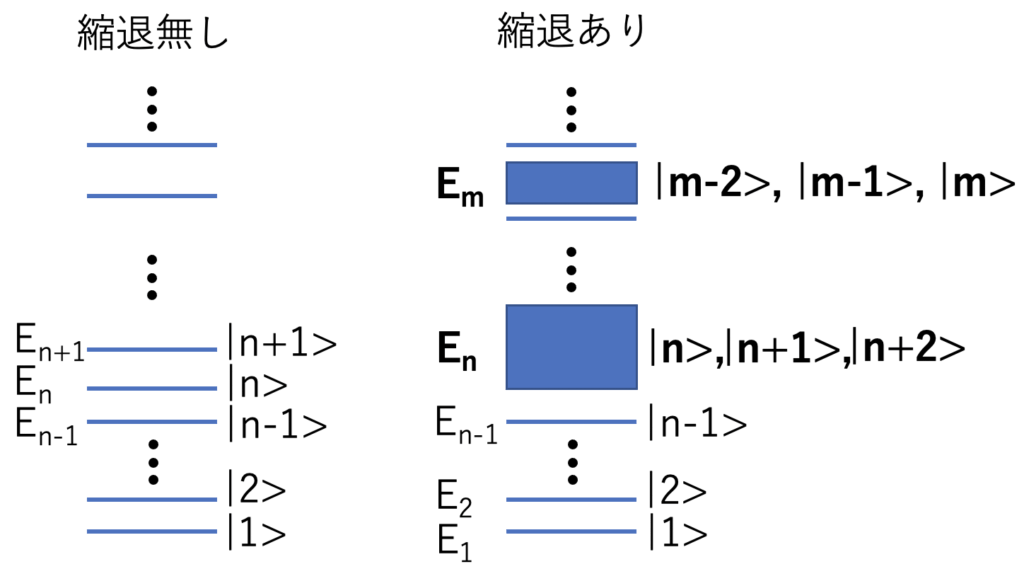
この右の例では2箇所で縮退が起きています。仮にψn-1を摂動展開しようと思えば、縮退がない時と全く同様に行えば良いです。しかし、ψn, ψn+1, ψm-2など、対応する初期状態で縮退が起きているような状態を摂動展開する時には注意しなくてはいけません。なぜなら、例えば、ψn+2を摂動展開する際、|n+2(1)>を{|n>}で展開するとします。すると、|n+2>と縮退している|n>と|n+1>の係数(|n+2>の係数はゼロ)に関しては1次摂動では決まらず、さらに1つ上の2次摂動を考えなくてはいけなくなるからです。ψmの時も同様で、|m(1)>を{|n>}で展開すると、|n+2>、|n>と|n+1>の係数は1次で決まるのですが、|m>と縮退している|m-1>と|m-2>の係数は今度は2次まで考えないと決まりません。
今回は、いくつもの箇所において縮退をもつ初期状態のうち、|n>に注目し、摂動によってどのように変化するかを追うことにします。なお、初期状態においてこの|n>は、|n1>, |n2>, …, |nN)>と縮退しているとします。
まずは、λの1乗の項の式を見てみます。縮退のない場合、この式から|n(1)>の{|n>}による展開及びEn(1)が分かるのでした。
H_0\ket{n^{(1)}}+H'\ket{n}=E_n\ket{n^{(1)}}+E_n^{(1)}\ket{n}縮退のない場合と同様に、まずはEn(1)を求めるために両辺で<n|との内積を取ってみます。すると
E_n^{(1)}=\bra{n}H'\ket{n}となります。つまり、縮退無しの場合と同じ結果が得られたわけです。
次に、|n(1)>を求めてみます。両辺、<k|(k≠n)と内積を取り、固有値を出して整理し
(E_n-E_k)\braket{k{\vert}n^{(1)}}=\bra{k}H'\ket{n}となります。ここで、集合Sを{n, n1, n2, …, nN}とすると、kがSの要素でないならば、En≠Ekなので、
\braket{k{\vert}n^{(1)}}=\frac{\bra{k}H'\ket{n}}{E_n-E_k},{\space} k{\notni}Sのように係数を求められます。しかし、2つ上の式で、kがSの要素ならば、En=Ekなので、左辺がゼロになってしまい、係数が求められません。更に、
\bra{k}H'\ket{n}=0,\space \forall_{k\ni S, k\not=n}という、基底に対する拘束条件もついてきます。この条件は、nをSの他の要素と入れ替えても同じことなので、
\bra{k}H'\ket{l}=0,\space \forall_{k,l\ni S,k\not =l}と拡張できます(注. |k∋S>で張られる部分空間において、H’が対角化されなければならない、という意味)。そこで基底をユニタリ変換し、何はともあれこの条件が満たされるようにしましょう。
上の話から、1次の摂動では|k>(k∋S)の係数が計算できません。どうしようもないので、そこで、2次の摂動
H_0\ket{n^{(2)}}+H'\ket{n^{(1)}}=E_n\ket{n^{(2)}}+E_n^{(1)}\ket{n^{(1)}}+E_n^{(2)}\ket{n^{}}を考えましょう。<k|(k∋S)と両辺で内積を取り、En=Ekを用いると、
\bra{k}H'\ket{n^{(1)}}=E_n^{(1)}\braket{k{\vert}n^{(1)}}となります。ここで、左辺について、{|n>}の完全性から、
\sum_{l\notni S}\bra{k}H'\ket{l}\braket{l\vert n^{(1)}}+\sum_{l\ni S}\bra{k}H'\ket{l}\braket{l\vert n^{(1)}}となります。左の部分については、すでに上で求めてある結果が使えます。右の部分は、4つ上の条件より、l=kの項のみ残ります。左辺右辺合わせて整理すると、
(E_n^{(1)} -E_k^{(1)})\braket{k\vert n^{(1)}}=\sum_{l\notni S}\bra{k}H'\ket{l}\frac{\bra{l}H'\ket{n^{}}}{E_n-E_l}となります(En(1)及びEk(1)は上での結果を使えます)。この式から、En(1)≠Ek(1)を満たすk∋Sについては、両辺を割って係数を出せます。もし、En(1)=Ek(1)となってしまうようなk∋Sが見つかってしまった場合は、そのような|k>での展開係数は求めることができず、更に3次の摂動まで考慮して係数を決定していきます(気力があれば、3次の結果も計算しようと思います)。


